New formulations and methods in flexible multibody dynamics
The Focus Group has achieved significant progress in two directions. A two-field formulation of the floating frame of reference method has been developed with the objectives of improved generality and enhanced numerical performance. Sensibility analysis to design parameters and performance optimization of flexible multibody systems has been performed using the adjoint variable method.


Focus Group: Multibody Systems
Prof. Michel Géradin (Université de Liège), Alumnus Hans Fischer Senior Fellow (funded by the Siemens AG) | Prof. Karin Nachbagauer (University of Applied Sciences Upper Austria), Alumna Hans Fischer Fellow (funded by the Siemens AG) | Daniel Lichtenecker (TUM), Doctoral Candidate | Dr. Valentin Sonneville (TUM), Postdoctoral Researcher | Host: Prof. Daniel Rixen (TUM)
Enhanced formulations for flexible multibody dynamics
The first and essential objective of this part of the project was to develop a fresh and more general approach to model reduction methods for flexible multibody dynamics, taking account of second-order effects in a simple and effective manner. For that purpose, the two-field formulation of the floating frame of reference method has been developed to construct reduced structural models [1,2]. It consists in a separate interpolation of the displacement and velocity fields, which leads to drastic simplification of the system kinetic energy. The adoption of a natural strain measure makes it possible to properly include geometric stiffening, even for reduced finite element models of flexible components.
The two-field model concept has been implemented in a rather general numerical environment (JuDyn) using the open-source programming language Julia, taking advantage of its unique features (e.g., modularity, strong variable typing, function polymorphism, JIT compilation).
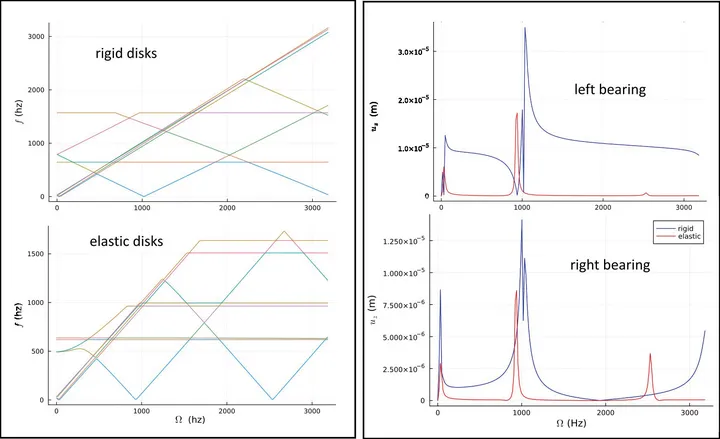
The two-field approach has been generalized to the dynamics of flexible multibody systems in a non-inertial frame [3], making it possible to address problems of rotor dynamics arising in mechanical and aerospace engineering (Fig. 1).
Figure 1
The method has also been extended to describe the inertial forces in nonlinear structural models such as beams [4] and shells [5] described in a geometrically exact manner [6].
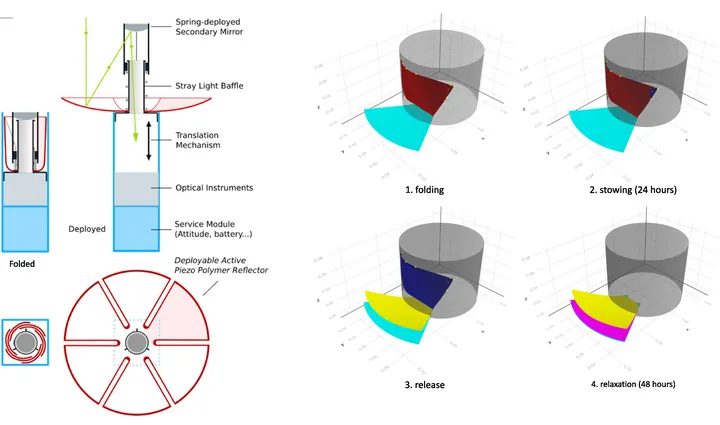
A large variety of numerical tests have been performed to verify the concepts, validate the JuDyn code, and evaluate its computing performance. The most significant test consisted in simulating the deployment in space of a polymer reflector prototype stowed inside a CubeSat [7] (Fig. 2). This benchmark required specific developments such as modeling of unilateral contact and extension of the shell model to viscoelasticity. The main outcomes of this part of the project are:
1) a set of papers published in peer-reviewed journals describing the theoretical concepts,
2) their implementation in the JuDyn package (https://github.com/michelg45/JuDyn.jl). The modularity of JuDyn makes it easily extensible for research and teaching purposes.
Figure 2
Optimal control strategies for robotic systems
This part of the project has focused on a digital twin for flexible robots, for intelligent and efficient control of robots for future scenarios of, e.g., human-robot interaction or surgery robots.
For this purpose, a method for smart control of the robot has been developed to meet various optimization goals, such as, e.g., to minimize the occurring joint forces or tension in flexible materials.
includes the solution of an optimization problem in multibody dynamics using the adjoint method. Since multibody dynamics systems often include highly nonlinear equations to describe also stiff problems, an efficient gradient strategy must be chosen for the optimization procedure to guarantee a fast but accurate update of the optimization variables. Therefore, adjoint gradients have been developed, with great success in both time-optimal and energy-optimal scenarios as compared to standard optimization strategies using numerical gradients. A comparison in function evaluations [8] has shown the superiority of the proposed adjoint gradients.
Moreover, in case future robots will include flexible components made, e.g., from composite or bio-inspired materials, the inverse dynamics problem will lead to the need for extensions of the gradients to account for elastic deformation as well as strain limits. Hence, a new adjoint gradient approach in flexible dynamics has been published recently and tested in a time-optimal two-arm flexible robot, as well as in an energy-optimal nonlinear pendulum [9]. Moreover, a discrete adjoint method for variational integration for optimal control of geometrically exact beam dynamics has been developed for constrained multibody systems [10].
The major outcomes of this part of the project are
1) a set of papers published in peer-reviewed journals describing the theoretical concepts for efficient optimal control in multibody dynamics,
2) their application for innovative flexible robotic systems, such as soft robotic fingers for reliable grasping (together with UC Berkeley [11]),
3) the spreading of the application of the method in the international multibody community through the organization of an IUTAM Symposium on the research topic of the Focus Group.
Figure 3
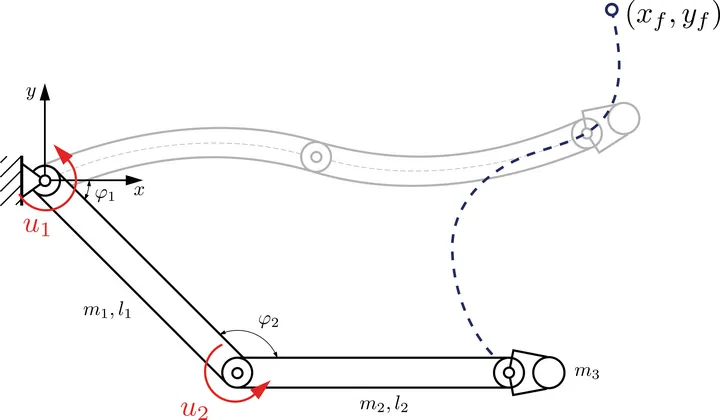
A follow-up MIRMI project on the combined optimal design and control of flexible multibody systems focuses on the application of our results for flexible robotic systems for modern medical robots, as in rehabilitation or prosthetic applications. Moreover, we have extended the methods for an application in medical tumor drug dosage using the optimal control with adjoint gradients [12]. Furthermore, another follow-up project on collaborative robotics will use the developed methods for safer, more reliable, and time-efficient human-robot-collaboration.
[1]
Géradin, M., Rixen, D.J. (2021).
[2]
Géradin, M. Dynamics of a flexible body: a two-field formulation. Multibody System Dynamics, 54(1), 1-29 (2022).
[3]
Géradin, M., Sonneville, V. (2024).
[4]
Sonneville, V., Géradin, M. (2022).
[5]
Sonneville, V. A geometric local frame approach for flexible multibody systems. PhD thesis, University of Liège. (2015).
[6]
Simo, J.C., Fox, D.D., Rifai, M.S. On a stress resultant geometrically exact shell model. Part I: Formulation and optimal parametrization. CMAME 72(3), 267–304 (1989).
[7]
Nielsen, C.J.G. et al. Actively Controlled Deployable Polymer Reflectors for Small Satellite Applications. 75th Int. Astronautical Congress (IAC) (2024).
[8]
Lichtenecker, D., Rixen, D., Eichmeir, P. & Nachbagauer, K. (2023).
[9]
Lichtenecker, D. & Nachbagauer, K. (2024).
[10]
Schubert, M., Sato Martin de Almagro, R.T., Nachbagauer, K., Ober-Blöbaum, S. & Leyendecker, S. Discrete Adjoint Method for Variational Integration of Constrained ODEs and Optimal Control of Geometrically Exact Beam Dynamics, Multibody System Dynamics (2023).
[11]
Lichtenecker, D., Yang, W.T., Nachbagauer, K., Tomizuka, M. Synchronization of Soft Pneumatic Actuators for Reliable Grasping, Proc. of the 7th IMSD, Madison, Wisconsin, USA (2024).
[12]
Eichmeir, P., Steiner, W. & Nachbagauer, K. The Use of Slack Variables in the Adjoint Method Handling Inequality Constraints in Optimal Control and the Application to Tumor Drug Dosage. Computational & Nonlinear Dynamics, 20(2): 021004(2025).
Selected publications
- Géradin, M., & Rixen, D. J. A fresh look at the dynamics of a flexible body application to substructuring for flexible multibody dynamics. International Journal for Numerical Methods in Engineering, 122(14), 3525-3582 (2021).
- Sonneville, V., & Géradin, M. Two-field formulation of the inertial forces of a geometrically-exact beam element. Multibody System Dynamics, 59(2), 239-254 (2023).
- Géradin, M., & Sonneville, V. A two-field approach to multibody dynamics of rotating flexible bodies. Multibody System Dynamics, 60(3), 375-415 (2024).
- Lichtenecker, D. & Nachbagauer, K. A discrete adjoint gradient approach for equality and inequality constraints in dynamics. Multibody System Dynamics, 61(1), 103–130 (2024).
- Lichtenecker, D., Rixen, D., Eichmeir, P. & Nachbagauer, K. On the Use of Adjoint Gradients for Time-Optimal Control Problems Regarding a Discrete Control. Multibody System Dynamics, 59(3), 313-334 (2023).
Full list of publications:
Prof. Michel Géradin
Prof. Karin Nachbagauer