Training neural networks without back-propagation
Finding neural network architectures and training networks pose big challenges in machine learning. We unravel novel architectures and propose new algorithms for training our neural networks. Particularly, our training algorithms do not rely upon gradient-based iterative optimization. We focus on solving time-dependent differential equations, both linear and nonlinear, using our neural networks.

Focus Group: Scientific Machine Learning
Prof. Wil Schilders (Eindhoven University of Technology), Alumnus Hans Fischer Senior Fellow (funded by the Siemens AG) | Chinmay Datar (TUM), Doctoral Candidate | Host: Prof. Hans-Joachim Bungartz (TUM)
Motivation and focus of the work:
Differential equations model diverse phenomena, from quantum systems to celestial motion, making the approximation of partial differential equations (PDEs) central to computational science. Traditional mesh-based methods such as finite differences, volumes, and elements are well established but face challenges with complex domains and high-dimensional problems. Artificial neural networks offer a promising, mesh-free alternative with high expressivity, the ability to handle high dimensions, and advanced tools for automatic differentiation. Yet significant challenges remain:
1) Finding appropriate neural network architecture: This typically involves extensive experimentation with a lot of trial and error and dealing with a high-dimensional hyper-parameter space, which can often entail significant computational costs.
2) Difficulties in training neural networks: The most pressing challenges in training neural networks are vanishing and exploding gradients, long training times, low accuracy, and inability to capture high-frequency temporal dynamics in the functions to be approximated.
The focus of our work has been on dealing with the two challenges outlined above.
Summary of the work carried out:
We categorize our work in three primary directions – (1) systematic construction of continuous-time neural networks, (2) sampling weights of deep neural networks, and (3) solving partial differential equations with sampled neural networks. Next, we summarize our contributions in each direction.
Figure 1
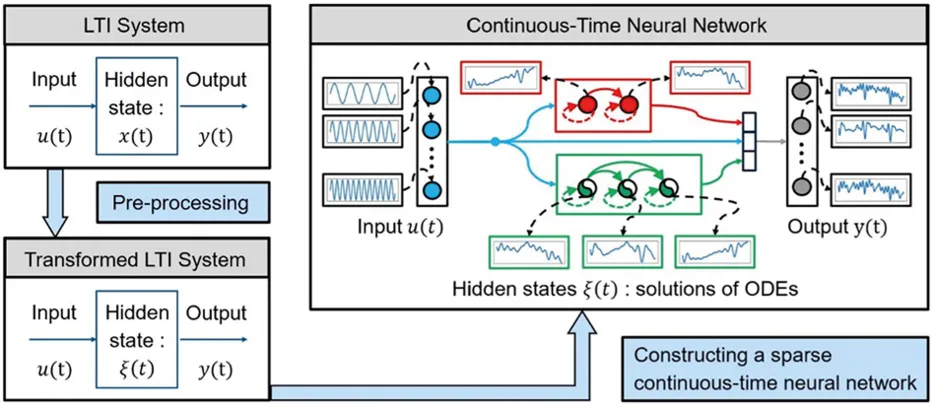
Datar, C., Datar, A., Dietrich, F., & Schilders, W. 2024a).
Systematic construction of continuous-time neural networks:
We developed a systematic method to design neural architectures for linear time-invariant (LTI) systems. [1] Using a variant of continuous-time neural networks, where neuron outputs evolve as solutions of first- or second-order ODEs, we introduced a gradient-free algorithm to compute sparse architectures and parameters directly from the LTI system. Our novel design features “horizontal hidden layers," in contrast to conventional "vertical” architectures, which may be less effective. We derived an upper bound for numerical errors and showcased the superior accuracy of our networks on various examples, including the 2-D diffusion equation (see Figs. 1 and 2).
Figure 2
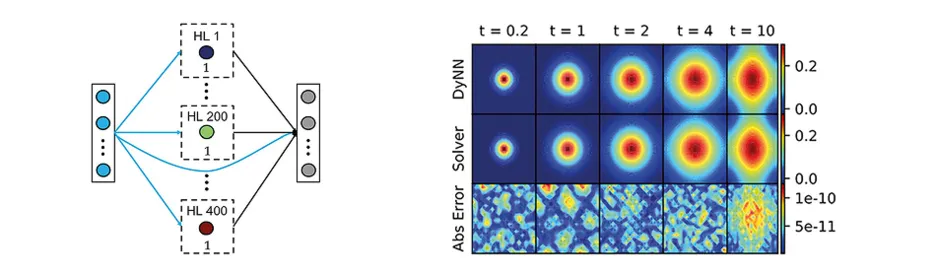
Sampling weights of deep neural networks (supervised learning):
In this direction, we first developed an algorithm for constructing neural network parameters by sampling them from certain data-driven distributions so that iterative updates are no longer necessary to obtain a trained network. [2] We demonstrated that the sampled networks achieve accuracy comparable to iteratively trained ones but can be constructed orders of magnitude more rapidly.
Solving partial differential equations with sampled neural networks (self-supervised learning):
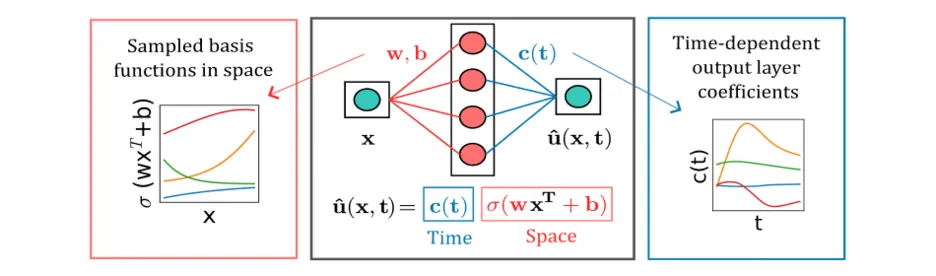
We extended our work on sampling network parameters to the setting of self-supervised machine learning problems in which one seeks to solve partial differential equations using neural network ansatz. [3] In this project, we addressed the challenges in training neural-PDE solvers and presented an approach to constructing special neural architectures and training our networks without back-propagation by integrating two key ideas: separation of space and time variables and random sampling of weights and biases of the hidden layers. We reformulate the PDE as an ordinary differential equation (ODE) using a neural network ansatz, construct neural basis functions only in the spatial domain, and solve the ODE leveraging classical ODE solvers from scientific computing. See Fig. 3 for an illustration of our approach. We later extended this work and used neural network ansatz to parameterize Hamiltonian functionsof energy-conserving systems [4].
Figure 3
Impact of the project:
Our work with continuous-time neural networks streamlines neural architecture design, reducing trial-and-error and cutting computational costs. These ideas can extend to embedding physics, such as two-body problem solutions, for approximating gravitational N-body systems. Sparse architectures are crucial for fast inference in edge computing, low-energy hardware, and real-time applications.
Our back-propagation-free algorithm outperforms gradient-based optimization in physics-informed neural networks, achieving faster training and greater accuracy – by up to five orders of magnitude. This enables neural PDE solvers to tackle complex real-world problems, overcoming challenges of limited accuracy and lengthy training times.
Future work:
The final outcomes of the project will serve as stepping-stones for multiple research directions in the future. We intend to extend our work with systematic construction of neural architectures [5] for more challenging classes of dynamical systems such as linear parameter-varying (LPV) systems, classes of parabolic PDEs with quadratic nonlinearities such as Burgers’ equation, and, ultimately, more involved nonlinear dynamical systems. We intend to extend our work in the direction of back-propagation-free neural PDE [6] solvers to gray-box settings and inverse problems, where parts of the PDE must be estimated, and high-dimensional problems with complicated solutions. We already have promising initial results in both directions and intend to publish these results in the coming months.
Final workshop
To mark the end of the Fellowship, a workshop was organized by Wil Schilders and Dirk Hartmann (Siemens): “Advancing scientific machine learning in industry.” The workshop was very well attended (> 120 participants), a considerable number from industry. The two-day workshop also had a panel discussion with panel members from different industries, and a working dinner to discuss a number of challenges faced in the area of scientific machine learning. This has led to a white paper that has been distributed to all participants and can serve as a starting point for further collaborations in the field of scientific machine learning.
In close collaboration with Prof. Felix Dietrich (TUM) and Dr. Dirk Hartmann (Siemens AG).
[1]
Datar, C., Datar, A., Dietrich, F., & Schilders, W. (2024a); Datar, C., Datar, A., Dietrich, F. & Schilders, W. (2024b).
[2]
Bolager, E. L., Burak, I., Datar, C., Sun, Q., & Dietrich, F. (2023).
[3]
Datar et al. (2024).
[4]
Rahma, A., Datar, C. & Dietrich, F. (2024).
[5]
Datar, C., Datar, A., Dietrich, F., & Schilders, W. (2024a); Datar, C., Datar, A., Dietrich, F. & Schilders, W. (2024b).
[6]
Datar et al. (2024); Rahma, A., Datar, C. & Dietrich, F. (2024).
Selected publications
- Datar, C., Datar, A., Dietrich, F., & Schilders, W. Systematic construction of continuous-time neural networks for linear dynamical systems. arXiv preprint arXiv:2403.16215 (2024a) (Accepted: SIAM Journal of Scientific Computing (SISC)).
- Datar, C., Datar, A., Dietrich, F. & Schilders, W. Continuous-time neural networks for modeling linear dynamical systems. In ICLR 2024 Workshop on AI4DifferentialEquations In Science. (2024b).
- Bolager, E. L., Burak, I., Datar, C., Sun, Q., & Dietrich, F. Sampling weights of deep neural networks. Advances in Neural Information Processing Systems 36 (2023): 63075-63116.
- Datar et al. Solving partial differential equations with sampled neural networks. arXiv preprint arXiv:2405.20836 (2024). (Under review: International Conference of Learning Representations (ICLR)).
- Rahma, A., Datar, C. & Dietrich, F. Training Hamiltonian neural networks without backpropagation. arXiv preprint arXiv:2411.17511 (2024) (Accepted: Machine Learning and the Physical Sciences Workshop at NeurIPS 2024).