In Focus:
Modeling ­Molecules 

Hans Fischer Senior Fellow Örs Legeza heads a research group at the Wigner Research Center for Physics in Budapest that focuses on “strongly correlated systems” – compounds and materials with unexpected and often useful properties. Legeza’s Host is TUM Professor Gero Friesecke, who uses mathematical tools to analyze, among other things, the electronic structure and dynamics of molecules. Their collaboration is pushing the envelope for simulations of quantum physical phenomena and extending the limits of what is  computationally feasible. They recently spoke with science journalist Patrick Regan.

Q: It’s easy to understand why it might be difficult to model molecules and materials. Why is it worth the effort? And is it within reach?
 

Legeza: In the history of all mankind, better understanding of materials always leads to a big change in society. Think about the stone age, bronze age, iron age, steam engines, electricity, semiconductors, nuclear technology – and now we see more and more emergent evolution in quantum technology. If we understand quantum technology, then we can manipulate other things on the atomic and nano scale. That means we may be able to understand and control some processes that lead to new products that can later change everybody’s life.

To understand how this is related to numerical simulations, think about how aircraft are designed and manufactured today. In the engineering world, nobody is building hundreds of actual models. Instead they do simulations on computers. When you design the new Airbus, for example, perhaps millions or hundreds of millions of simulations are performed on the different parts before the computer suggests solutions that seem to be the best. It’s only then that people start to build the actual models and put them into wind tunnels and perform other tests to measure whether the parameters match with the computer simulations.

In a chemical reaction path, there are many intermediate steps as you go from system A to system B. If you could selectively model and manipulate key steps, there would be many potential applications. We want to do the simulations in the same way as in the classical world, just like with these CAD programs in engineering. It would be good to have something like a quantum CAD to do all these things.

In quantum physics, we are not at this stage yet. We understand many things, but there are still many things that we can’t describe, or we don’t have complete knowledge about. But the kind of knowledge that we already have, this we can program. That is exactly what people are doing in computer simulations for quantum systems.

Q: And one of your main tools, and a focus of your research, is an equation that was devised and published around a hundred years ago?

Friesecke: Yes, the Schrödinger equation. The reason Erwin Schrödinger invented it is the same reason we’re still studying it today. He wanted to be able to make predictions about the behavior of atoms and molecules and materials. They have a life of their own. They’re not just dead objects. They act, they move, they perform tasks. They keep the world running. They keep biology running. And the quickest access is often through theory, because sometimes you can’t access what they’re doing with experiments.

A good example is FeMoco, short for iron-molybdenum cofactor, which plays the crucial part in nitrogenase. That’s the enzyme used by microbes, which often live in symbiosis with plants, to take nitrogen out of the air and “fix” it, transforming it into plant food. Plants can’t use N₂ from the air. It needs to be broken apart to form NH₃, ammonia.

Q: I can’t tell you how many times scientists have told me that plants are the best chemists in the world.

Friesecke: I agree with that. You can use the Haber-Bosch process to make ammonia – under high heat and pressure – in the lab or on an industrial scale, but that requires a huge amount of energy. Or you can put your plant in the sun on the balcony, and the enzyme just makes it happen. How? With better understanding, it should be possible to emulate this and drastically reduce the cost of fixing nitrogen. As we reported in a paper published in a computational chemistry journal, Örs managed to do a good simulation of the enzyme’s quantum electronic structure that could shed some light on this.

Legeza: This is “only” a simulation of the electron cloud of the enzyme by itself. Simulating a whole dynamic process like nitrogen fixation, which involves the interaction of the enzyme both with the N₂ molecules in the air and other parts of the environment, is one of the great future challenges. 

Friesecke: That enzyme is a pretty big beast. Until very recently there was a disconnect between this world of theory, with the Schrödinger equation, and the world of living things and interesting biomolecules that perform tasks. At the quantum resolution, it wasn’t possible to do a Schrödinger equation simulation. Each time you add a particle, the computing time doubles, and doubles again, so this has been like a brick wall.

People in the field of quantum chemistry had already done the first simulation of an atom in the 1920s. But an atom is not so interesting for chemistry. It’s just a basic building block. By the 1960s, people got to maybe benzene, and by the 1980s they were still stuck at benzene. You really need high accuracy to resolve the behavior to the scale where interesting transitions happen, where bonds break, and if you want to simulate that reliably you need the Schrödinger equation.
 

Q: Over all the decades before the advent of powerful computers and clever algorithms, how did researchers approach this?

Friesecke: I would say there were two schools. There were the exact modelers, and there were the simplifiers. And the first group was saying, we need to stick with the equation. We only make some very careful approximations that are not too crude, and then we can simulate small systems. And then there was the second group who said, oh, no, the equation is too complicated. Let’s remodel it, get a simplified model, and then run simulations of complex systems – so we’re going to lose accuracy, but we can predict something about, say, a metal surface or a metal-organic compound.

These two schools both got the Nobel Prize in 1998. From the precise school, it was John Pople, who started the first computer program which is the ancestor of today's programs like Örs’s but for much smaller systems. He could simulate things like benzene with some accuracy. And the other was Walter Kohn, the founder of a field called density functional theory. This relied on a cruder approximation of the Schrödinger equation but could be extended to a thousand particles or so. It wasn’t 100 percent reliable, but it gave a lot of good insight into what’s happening. So the Nobel committee was wise and gave the prize to both.

 

Q: That was for work done over what period of time?

Friesecke: The award was for 30 years of cumulative work by the community, starting in the 1960s, and two of the founders got the Nobel Prize – the first ever given for computational quantum mechanics.

It’s only due to cumulative advances in the past 20 years that this brick wall is beginning to be cracked, between the Schrödinger equation and getting to the size of interesting biomolecules. I think we made a big advance in simulations of such systems at chemical accuracy.

 

Q: So two of your own stated goals are accuracy and efficiency. If you’re measuring efficiency in terms of computing resources, that seems fairly straightforward. But how do you gauge the accuracy of a simulation?

Friesecke: That’s very easy. Experimental data. The thing that distinguishes the different quantum states of a molecule is the energy level. The level the system adopts when you don’t have any external forces is the lowest energy state. And energy can be measured from spectroscopy, so we have wonderfully accurate measurements by five, six, seven, eight digits. At the end, you really benchmark against experiment.

In quantum science, the accuracy of data on the real-world energy level is fantastic. The trouble is, you know the energy level of the molecule, but you don’t know the quantum state. So you measure just the energy. That’s the check you use. The methods are constantly competing against the measurements, and if you get the third digit wrong, you’re out. It makes a big difference which state a system is in, ferromagnetic or non-magnetic, polarized or not polarized, rotated this way or that way. Especially in designing chemical reactions, the accuracy has to be good enough to decide which reaction path the system is actually taking. And that dictates to how many digits you want for the energy levels. It’s not like chasing the hundredth digit of Pi, but you want them accurate enough to distinguish different transition paths and different quantum states.

Q: So the methods that you’re using can make this kind of detail accessible?

Friesecke: Exactly. I would say that is where Örs is one of the pioneers in bridging the two schools. He brings much bigger systems within the reach of this kind of chemical accuracy. 

Legeza: Maybe there are originally these two worlds, physics and chemistry. I’m coming from physics. In physics we are looking at very complicated systems, and we want to make a model that can describe a physical process. For example, if you tune the temperature or the magnetic field or the pressure, you see some kind of change in the material properties. You can for example show that the magnetic properties change. In physics, we are very happy if we can show the material properties change, even if the transition temperature that we calculate is far off. It still can give you good qualitative descriptions. If you want to fine-tune it, then you have to refine your models, and you have to take a far more accurate and precise approach – and this is what comes from the quantum chemistry side.

The two worlds are coming together now. In physics you can study very large models with less precision and still get a good description of many things. In the quantum chemistry world, you really describe these energetic properties and other things on a very accurate scale. And of course if you can do larger and larger simulations, you can improve the models and model larger systems. The two will approach each other at some point.

This is why my code for computer simulation has both features. It is flexible, because we   are using it for model systems in physics, but I’m also applying it to quantum chemistry. You can fine-tune these two approaches and use the extreme power of the machines that we have nowadays. You get improvements in speed of a factor of tens, hundreds, thousands, so that you have the chance to study larger systems or more accurate models. This is how things advance, step by step.

 

Q: What are the most serious issues limiting further progress?

Legeza: One major issue is scaling. Richard Feynman said that when simulating quantum systems on classical computers, the problems scale exponentially with the system size and complexity. Of course a quantum computer could solve this, breaking down this complexity issue. But what Gero and I and many others in math and physics are doing is to design mathematical algorithms that by some approximation can help us bring down this exponential scaling to the so-called polynomial form. For people who are coming from other fields, exponential refers to a function that increases extremely rapidly, and polynomial to a function that is manageable using computers available today.

Once you have the algorithm, then the question is how to implement it on the latest modern technology from IT and computer science. And if you do this, then you can further speed up this polynomial form, and that is exactly what we’re doing.

Friesecke: It makes a huge difference which way you run an algorithm. You can do it in a basic way. You can do it in a smart way. Every algorithm we have now could be made to run in an even better way. And the best implementation depends on the hardware, and that’s one of the reasons I admire Örs so much. He’s a modern interdisciplinary scientist, a physicist who can talk about the mathematics of the algorithms with me and then talk with people from NVIDIA and AMD about how to implement these methods on their new hardware – machines that are not based on CPUs, but rather on GPUs, graphics processing units. 
 

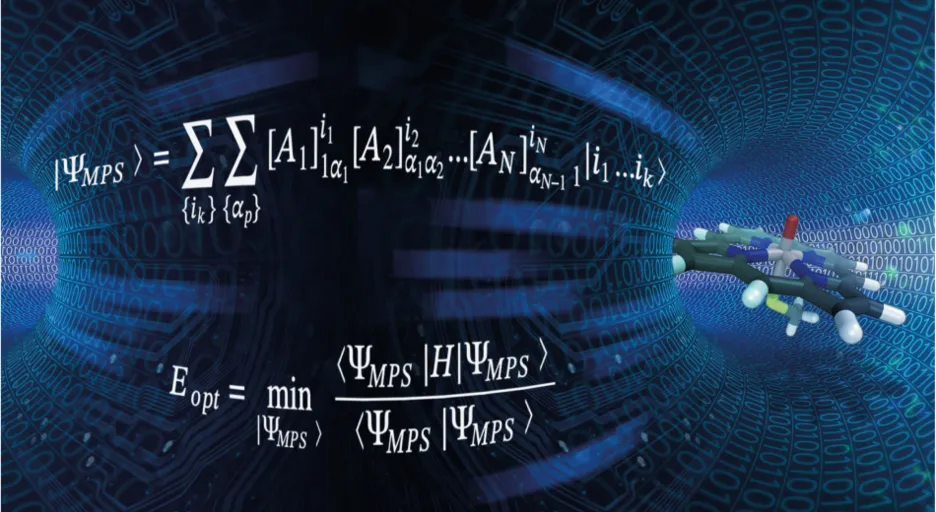
Q: This could be interesting to a number of different industries, right?

Legeza: It has many aspects. Accurately simulating the behavior of larger systems could eventually be valuable for a range of applications, from biological research to industrial catalysts and pharmaceuticals. Perhaps the most immediate benefit, however, is that our algorithms can help advanced computer manufacturers test and improve their technology. For example, I did some calculations that helped NVIDIA to validate some of their very recent developments on both the hardware side and the software side. They even mentioned us in an announcement. So not only is the algorithm a tool to run simulations in chemistry or physics, but it’s also contributing in computer science to benchmark efficiency of hardware.

Friesecke: It’s a two-way interaction, where these hardware companies, NVIDIA, AMD, and others, also need users who provide feedback which can help them optimize their design. 

Legeza: With Gero, these mathematical algorithms are very well controlled in terms of math, so you can really have very direct means of accessing the accuracy, and there are many things that you can fine-tune by changing the parameters. It’s not just a matter of running a calculation and getting something out. Physics, chemistry, and math – everything comes together. We can focus on the mathematical properties and the detailed analysis. And if you have this, you can validate all the calculations and also provide immediate benchmarks for the industry.

 

Q: Your work on algorithms, to make models more efficiently computable, strikes me as being analogous to the crucial role of information theory in making the most of technological advances such as semiconductor lasers and optical fibers. Is that a valid way of looking at it?

Friesecke: Absolutely. It’s 100 percent accurate. You have the two sides. You need to compactly encode the information. There are millions of parameters, and many of them are important, but you don’t know in advance which ones. You pick the right encoding of the information to capture the important pieces and then process that. And then at the same time you need the hardware. The hardware technology and the efficient encoding of the information, they have to be advanced together. I would say it’s 50-50. Sometimes you gain by better encoding and processing of the information, and sometimes you gain by changing the hardware.

 

Q: Could you explain how the so-called tensor network methods make this possible?

Friesecke: In a sense these tensor network methods try to split up a very high-dimensional problem, which means you have many unknown parameters. It tries to split it up into many smaller problems with fewer parameters. And then these smaller problems communicate with each other across the edges of some graph. So then there are many issues that could be optimized. One is the design of the size of the blocks in which you split up the big problem. Then which pieces need to communicate with which other pieces. And then  at which accuracy do you need to resolve the individual pieces and then bring these together at the end to get the results.

There’s one way in which Örs is different from other researchers who use these methods. We met in 2018, at a meeting in Berlin. Örs was the only speaker who talked about these methods in a very global way. People have done really important work, but usually they focus on one ingredient and optimize that. Örs was saying look, we have to optimize all these things together. So his code constantly adapts the size of the sub-problems, how they are connected, the basis functions, and so on.

 

Q: What kinds of measurements can help you gauge your own progress?

Legeza: There are, for example, computational benchmarks for running simulations of quantum systems, measured nowadays in petaflops, quadrillions of floating point operations per second. It’s well known that we are still not using all the available computational power. Even now, although together with my colleague Andor Menczer we have, in collaboration with industrial partners and Pacific Northwestern National Laboratory, reported the largest calculation on a single computational node, we are still nowhere if we talk about exascale computing and the possibility of achieving 1,000 petaflops.

Now if we put together 40 such machines, we immediately reach the full capacity of the most powerful supercomputer of a decade ago. This is a difficult problem, but the technology is around us, and improvements in mathematics are also around us. Physicists came up with powerful methods, Gero and others are actively working on the mathematical aspects, and there are also some algorithmic ideas that can improve the mathematical scaling. Math and physics, that’s not enough alone, you have to include computer science, and if you put everything together, then you can win the game.

 

Q: How does the prospect of quantum computing fit into this picture?

Legeza: When you focus on how to optimize algorithms on the current, classical hardware, this is a mathematical issue. Thinking about how to implement the algorithms in a different way on different hardware, that’s a technical issue. But a third issue is how this connects to quantum computing. All the simulations we are doing are immediately connected to quantum information theory and quantum computing, so it all goes hand in hand.

I think it’s safe to say that there is no universal quantum solver. So once quantum computers will work to solve real-life problems, there will be very specialized, specially optimized quantum algorithms for different tasks. In this kind of task, of course, the superiority of the quantum computer is not questionable. On the other hand, we have the classical algorithms, which we can adapt to solve problems over a broad range, and then of course improve step by step. Where is the border, the edge, between the two?

Maybe there’s a set of problems that are accessible by quantum computers in a much better way, a set of problems that are still more accessible by classical computers, and a third possibility: creating hybrid algorithms. That is, we could use classical computers to ­prepare inputs for quantum computers, or to do pre- or post-processing of quantum computer ­simulations. 
 

Q: Would you like to comment on the role of the TUM-IAS in fostering the kind of collaboration you’ve been describing?

Friesecke: The TUM-IAS is a rare thing. When we wrote up our proposal, it was seen as an advantage that it connects two fields. There’s a big gap in support for this kind of work, ­because it’s high risk but also potentially high reward. Funding agencies all claim they like high-­risk / high-reward, but if you look at the decisions, what is the project list? It’s almost always on the conservative side. The ­TUM-IAS should keep it their way, promoting new collaborations between people from different disciplines. 

Legeza: The financial support from this program has been very important, and so has the way the TUM-IAS brings people together to exchange ideas. I’m now involved in a number of other collaborations, with other institutions, that were made possible in part by this Fellowship. And because the Fellowship supports a PhD position, that is also a way to ensure knowledge transfer, and this person can go abroad and expand the research network. There is also support for holding workshops, which we did in April 2024, bringing together experts from here and overseas. So the TUM-IAS not only represents a community, but also stimulates further interactions. All these aspects are important: encouraging knowledge exchange and travel, as well as supporting the younger generation.