Coding and cryptography for privacy, security, and storage

Post-quantum cryptography

Post-quantum cryptography, in particular code-­based cryptography, promises to guarantee security even when capable quantum computers will break most classical public-­­key cryptosystems. In this collaboration, we have studied code-based cryptography in both Hamming and rank metrics.

We have derived a polynomial-time key recovery attack for a McEliece-type ­cryptosystem based on twisted Reed-Solomon codes, which proves that the proposed system is insecure. For the Hamming Quasi-Cyclic (HQC) proposal, which is a promising candidate in the third round of the NIST Post-­Quantum cryptography standardization project, we have shown that, utilizing a power-side channel, we are able to mount an efficient key-­recovery attack, which indicates that the ­proposed implementation of the system is not secure [1]. Further, we have investigated how so-called hints that stem from side-channel attacks reduce the work factor of general ­information set decoding algorithms [2].

Recently, we have focused on the rank ­metric, which allows the development of systems with smaller key and ciphertext sizes. ­Thereby, we have proposed and analyzed a new algorithm to solve the problem of decoding errors of rather large rank-weight with Gabidulin codes [3]. The complexity of this problem is of importance to assess the security of rank-metric code-based cryptosystems. Further, we have extended a cryptosystem based on Gabidulin codes where we modified the encryption and decryption algorithms of Loidreau’s cryptosystem in order to achieve smaller key sizes. Besides Gabidulin codes, low-rank parity-check (LRPC) codes are very interesting for code-based cryptography due to their weak algebraic structure; therefore, we have defined and studied LRPC codes and their decoding over Galois rings [4]. The most important contribution here is that we have proposed a new a new code-based cryptosystem, called LIGA, based on the hardness of list decoding Gabidulin codes.

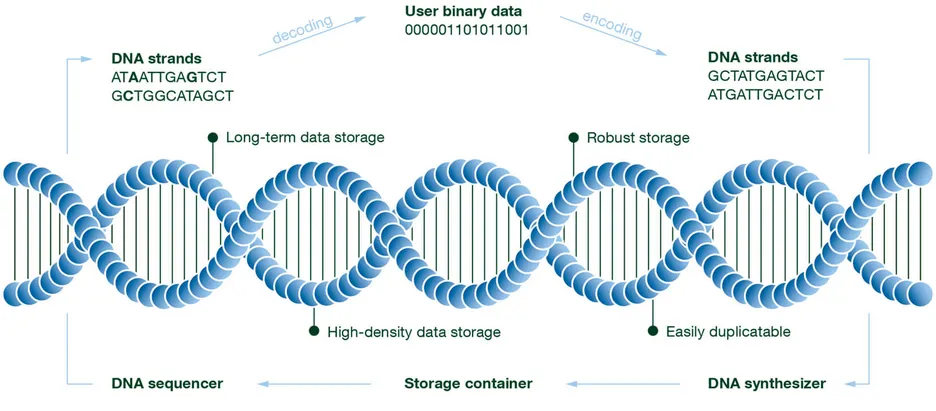
Coding for DNA storage

DNA-based data storage, as shown in Figure 1, consists of DNA synthesis as the writing process, storage in a special storage ­medium, and DNA sequencing as the reading process. In contrast to conventional storage methods, due to the nature of DNA and the biological processes involved, special error patterns such as insertion, deletion, and substitution errors occur.

We have studied fundamental storage density limits of DNA storage systems [5]. These findings are among pioneering work that aims to provide guidelines on how to ­design error-correcting codes for the systems. Further, we provide code constructions that achieve high storage rates and allow for time-efficient decoding.

In terms of explicit error-correcting codes for DNA storage, we designed a code optimized to correct a combination of error types. As the combination of different error types is hard in general, we first focused in a first step on a code construction for a single deletion and a single substitution [6]. Furthermore, we have studied a new type of deletion error patterns: crisscross deletion patterns. ­Given an array where several rows and several columns are deleted or inserted, we aim to reconstruct the original array by introducing a certain underlying structure in the original arrays. Error-correcting codes for bursts of insertions and duplications, two types of errors frequently occurring in DNA storage systems, are presented in two more of our papers. We have also studied covering codes for insertion and deletion errors. The results are useful to design and analyze ­massively parallel clustering algorithms of synthetic DNA strands. We have further investigated codes that facilitate and speed up clustering algorithms by using “clustering-correcting codes” [7]. These codes further improve the accuracy of the clustered sequences.

Another focus was on codes over sets which lay the foundation for error-correcting codes in DNA storage systems as they protect  ­unordered strands from vectors [8]. Our results allow on the one hand to understand ­
the fundamental rate-limits of DNA storage systems and on the other hand provide ­efficient codes that allow for error correction of typical errors that arise in DNA storage.

One of the most costly bottlenecks of DNA-based data storage, in terms of cost and time, is the synthesis process. We have therefore shown how to add redundancy to DNA strands to allow for a faster and less ­costly synthesis [9]. In particular, for synthesis ­machines that synthesize a massive amount of DNA strands in parallel, we show how to save ~50 % in time and synthesis material as compared to conventional methods.

Coding for distributed data storage and private information retrieval

The huge amount of data that is constantly being processed has led to the construction of huge data centers spread over different locations. Each of these data centers ­consists of a network of storage disks or servers where the data is distributed among the ­servers. However, given the massive number of storage servers, server failures happen frequently. Therefore, it is necessary to store redundant data alongside the initial data via a storage code.

With the increase in usage of distributed services such as cloud storage and peer-to-peer networks, the importance of user privacy is constantly on the rise. Recently, private information retrieval (PIR) in the context of coded storage has gained a lot of interest. With PIR, a user is able to download a desired file from a database or distributed storage system (DSS) without revealing the identity of the file to the servers (see also Figure 2).

In this collaboration, we first have proven the capacity for DSS that are protected against server failures by erasure codes for the use case where the user is only supposed to learn exactly what is desired, which is referred to as symmetric private information retrieval (SPIR).

In another work, the star product scheme has been adopted, with appropriate modifications, to the case of private (e.g., video) streaming [10]. It is assumed that the files to be streamed are stored in a distributed ­manner over several servers by an erasure code, and the download is carried out in a manner suitable for streaming applications.

Further, we have focused on how to optimally repair a certain number of failed servers by contacting the least number of other servers [11]. We have derived the trade-off between the redundancy and the failure tolerance of a storage system when the number of repair servers changes according to the number of failed servers. Moreover, this class achieves the best trade-off between redundancy and failure tolerance with this repair property.

[1]
Schamberger, T., Renner, J., Wachter-Zeh, A. & Sigl, G. A Power Side-Channel Attack on the CCA2-Secure HQC KEM. CARDIS (virtual), 2020.

[2]
Horlemann, A.-L., Puchinger, S., Renner, J., Schamberger, T. & Wachter-Zeh, A. Information-Set Decoding with Hints. CBCrypto (2021).

[3]
Renner, Jerkovits, T. , Bartz, H., Puchinger, S., Loidreau, P. & Wachter-Zeh, A.Randomized Decoding of Gabidulin Codes Beyond the Unique Decoding Radius.  International Conference on Post-Quantum Cryptography (PQCrypto), 2020, Paris, France.

[4]
Renner, J., Puchinger, S., Wachter-Zeh, A., Hollanti, C. & Freij-Hollanti, R.. Low-Rank Parity-Check Codes over the Ring of Integers Modulo a Prime Power. IEEE Int. Symp. Inf. Theory (ISIT), 2020, Los Angeles, USA.

[5]
Lenz, A., Siegel, P., Wachter-Zeh, A. & Yaakobi, E. Achieving the Capacity of the DNA Storage Channel (Invited Paper). International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2020, Barcelona, Spain.

[6]
Smagloy, I., Welter, L., Wachter-Zeh, A. & Yaakobi, E. Single-Deletion Single-Substitution Correcting Codes. IEEE Int. Symp. Inf. Theory (ISIT), 2020, Los Angeles, USA.

[7]
Shinkar, T., Yaakobi, E., Lenz, A. &Wachter-Zeh, A. Clustering-Correcting Codes. IEEE Trans. Inform. Theory vol. 68 / no. 3 (2021).

[8]
Lenz, A. et al. (2020).

[9]
Lenz, A. et al. Coding for Efficient DNA Synthesis. IEEE Int. Symp. Inf. Theory (ISIT), 2020, Los Angeles, USA.

[10]
Holzbaur, L. et al. (2020).

[11]
Holzbaur, L. et al. (2021).

Selected publications

• Holzbaur, L., Puchinger, S., Yaakobi, E. & Wachter-Zeh, A. Partial MDS Codes with Regeneration. IEEE Trans. Inform. Theory vol. 67 / no. 10, 6425–6441 (2021).
• Renner, J., Puchinger, S. & Wachter-Zeh, A. LIGA: A Cryptosystem Based on the Hardness of Rank-Metric List and Interleaved Decoding. Designs, Codes, and Cryptography 89, 1279–1319 (2021).
• Lenz, A., Siegel, P., Wachter-Zeh, A. &Yaakobi, E. Coding over Sets for DNA Storage. IEEE Trans. Inform. Theory vol. 66 / no. 4, 2331–2351 (2020).
• Holzbaur, L., Freij-Hollanti, R., Wachter-Zeh, A. & Hollanti, C. Private Streaming with Convolutional Codes. IEEE Trans. Inform. Theory vol. 66 / no. 4,2417–2429 (2020).
• Etzion, T. & Wachter-Zeh, A. Vector Network Coding based on Subspace Codes Outperforms Scalar Linear Network Coding. IEEE Trans. Inform. Theory vol. 64 / no. 4, 2460–2473 (2018).

Full list of publications