Interconnections that govern crucial aspects of our lives
Many systems that govern our lives – from transportation networks to the human brain – can be seen as networks of interconnected dynamical units. The coordinated dynamics of all units, such as synchronization, are intricately linked to the system function. This Focus Group develops fundamental insights into factors that determine network dynamics to elucidate the function of real-world networks and to design effective interventions in case of malfunction.


Focus Group: Network Dynamics
Prof. Krasimira Tsaneva-Atanasova (University of Exeter), Alumna Hans Fischer Senior Fellow | Prof. Christian Bick (Vrije Universiteit Amsterdam), Alumnus Hans Fischer Fellow | Tobias Böhle, Elena Gonzalez Herrero (TUM), Doctoral Candidates | Host: Prof. Christian Kuehn (TUM)
(Image: Alain Goriely (Bick))
The function of systems of interconnected dynamical units – for example, the human brain, which contains billions of individual neural cells – depends on their emergent dynamical properties. Collective dynamics in networks, such as synchronization, where individual units behave in unison, is intricately linked with the function of these networks. Indeed, coordinated beating of heart cells makes the heart function, while excessive synchrony in the human brain is associated with malfunction and disease. The Focus Group Network Dynamics gains fundamental insights into the factors that govern the collective dynamics of coupled dynamical units, over both short and long time scales. Our results cover both fundamental mathematical theory (such as bifurcations in dynamical systems) and applications to models relevant for real-world networks such as the human heart and brain to build the basis for new intervention techniques to restore healthy function.
Having many interconnected dynamical units is a common feature of systems with complex dynamics. For example, the human brain consists of billions of interconnected neuronal cells. The sheer number of units, however, is an obstacle to obtain mathematical insights. Hence, methods to reduce the complexity and dimensionality of the problem become crucial to understand how, for example, synchrony emerges in these network dynamical systems. In Ref. [1], we develop new approaches for phase reduction, a complexity reduction technique that is applicable to networks where each unit is oscillatory. Our theoretical approach elucidates two important aspects. First, we clarify how the geometry of the oscillation affects the synchronization behavior of the network dynamical system. Second, our technique is applicable beyond commonly applied first-order approximations that are only valid for very weak coupling. In particular, it highlights how (and what) nonpairwise nonlinear phase interactions, that is, interactions between three or more units, arise in the reduced network that may be relevant for synchronization behavior if the coupling is stronger.
If network function is linked to synchronization behavior, it is critical to understand whether synchronization persists as the system parameters are varied. For example, only sufficiently strong coupling may lead to synchronization of oscillators with distinct frequencies. Transitions in synchronization behavior can be continuous (a small change in a parameter leads to a small change in the synchrony properties) or discontinuous (small changes can lead to jumps in synchronization behavior – in the latter case, such synchronization transitions are also known as “explosive” transitions due to the rapid change in system dynamics. In phase oscillator networks, for example, explosive transitions can be observed when nonpairwise, higher-order interactions (which become relevant for stronger coupling) are present. Using an approach from bifurcation theory in Ref. [2], we uncover a universal route to explosive transitions in dynamical systems by showing that variations of generic system parameters can turn a continuous transition into a discontinuous transition. This not only explains how nonpairwise interactions lead to explosive synchronization transitions, but also shows that it is not specific to these nonpairwise interactions but rather a universally expected effect.
Figure 1
Apart from these universal results, we obtained further insights for specific examples of oscillator networks with a given coupling structure. In Ref. [3], we consider ring-like networks of phase oscillators that give rise to rotating wave solutions – think of synchrony in the form of a merry-go-round or a wave in a stadium. We showed that nonpairwise higher-order interactions can stabilize such solutions, an insight that is beneficial if one wanted to control synchrony in these systems. Moreover, we show that nonpairwise interactions can also turn a continuous transition away from a uniform rotating wave solution to an explosive transition – in line with the universal results expected from our previous research in Ref. [2].
Figure 2

Interactions between individual units are crucial for the functioning of systems that we depend on in our daily lives: Electric signals between excitable heart cells called cardiomyocytes are vital for making the heart contract properly, which is essential for its healthy functioning. By contrast, signaling going wrong can lead to heart problems such as irregular heartbeats (arrhythmia). It is hence crucial to explore different methods to better understand how these heart cells transmit signals, with the goal of finding ways to improve medical treatments. Heart cell behavior is complex and difficult to study using rigorous mathematical analysis. In Ref. [4], we compare two simpler models that capture the important aspects of how heart cells work: One mimics how heart cells get excited (the FitzHugh–Nagumo model), and the other is made specifically to mimic heart cells’ excitable behavior (the polynomial Karma model). We employ geometric singular perturbation theory to study the dynamical properties of the models. We also look at how these models act in a one-dimensional space, studying excitable wave propagation. Finally, we run computer simulations to see how changing certain aspects of the models affects how the waves propagate. Our study helps us understand what these models have in common and what makes them different.
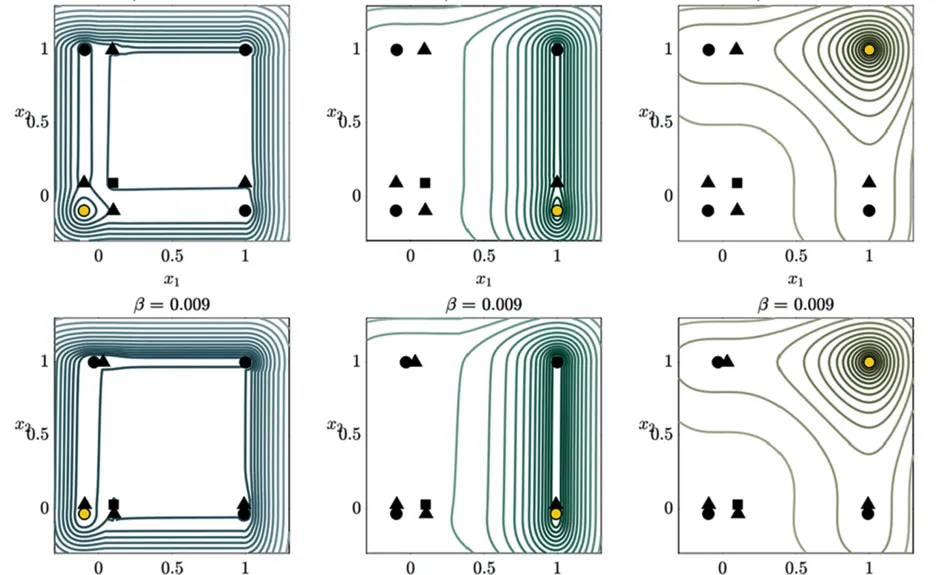
Brain networks can transition between synchronized and desynchronized states, reflecting various cognitive and physiological conditions in health and disease. Elucidating these transitions is essential to understand healthy brain function. Our focus is on understanding transitions from a “quiescent” to an “active” attractor in networks of multi-stable systems in the presence of random noise. Coupling such systems leads to qualitatively different transient behaviors depending on the coupling strength. With weak coupling, transitions are stochastic, while strong coupling promotes synchronous transitions, which we called a “fast domino” regime. An intermediate regime, called a “slow domino,” shows transitions that can be arbitrarily long. Our previous work has described transition timings and sequences using potential landscape bifurcations in the low noise limit. In Ref. [5] we now examine noise-induced transitions employing a quasipotential (QP) in scenarios where the coupled system lacks potential, as is often the case in models of real-world systems. Gates, represented by points on the boundary of the basin of attraction with minimal QP concerning the attractor, help characterize the escape rates from the basin. However, alterations in the coupling strength can cause these gates to undergo a global shift. This global gate-height bifurcation marks a general qualitative change in the escape characteristics of parameterized non-gradient dynamical systems subject to small noise.
Figure 3
[1]
Bick, C., Böhle, T. & Kuehn, C. (2023).
[2]
Kuehn, C. & Bick, C. (2021).
[3]
Bick, C., Böhle, T. & Kuehn, C. (2023).
[4]
Gonzalez Herrero, M.E., Kuehn C. & Tsaneva-Atanasova K. (2021).
[5]
Ashwin P., Creaser J. & Tsaneva-Atanasova K. (2023).
Selected publications
- Bick, C., Böhle, T. & Kuehn, C. Higher-Order Network Interactions through Phase Reduction for Oscillators with Phase-Dependent Amplitude. ArXiv (2023). www.arxiv.org/abs/2305.04277.
- Kuehn, C. & Bick, C. A universal route to explosive phenomena. Science Advances 7(16), (2021). www.doi.org/10.1126/sciadv.abe3824.
- Bick, C., Böhle, T. & Kuehn, C. Phase Oscillator Networks with Nonlocal Higher-Order Interactions: Twisted States, Stability, and Bifurcations. SIAM Journal on Applied Dynamical Systems 22(3), 1590–1638 (2023). www.doi.org/10.1137/22M1500940.
- Gonzalez Herrero M. E., Kuehn C. & Tsaneva-Atanasova K. Reduced Models of Cardiomyocytes Excitability: Comparing Karma and FitzHugh–Nagumo. Bulletin of Mathematical Biology 83(8), 88-88 (2021). www.doi.org/10.1007/s11538-021-00898-0.
- Ashwin P., Creaser J. & Tsaneva-Atanasova K. Quasipotentials for coupled escape problems and the gate-height bifurcation, Phys. Rev. E 107(1), (2023). www.doi.org/10.1103/PhysRevE.107.014213.
Full list of publications:
Krasimira Tsaneva-Atanasova
Christian Bick
