New paradigms for optimal transport
Optimal transport is a rich and deep mathematical theory, primarily concerned with studying the best way to move available resources to a target configuration of destinations. In our Focus Group, we developed new frameworks for theoretical and computational investigations that greatly extend the scope of the theory, with promising applications to other relevant branches of mathematics.

Focus Group: Optimal Transport in Science, Technology and Society
Prof. Giuseppe Savaré (Bocconi University), Alumnus Hans Fischer Senior Fellow | Dr. Giacomo Enrico Sodini (TUM, now University of Vienna), Doctoral Candidate | Hosts: Prof. Massimo Fornasier, Prof. Daniel Matthes (TUM)
(Image: Bocconi University)
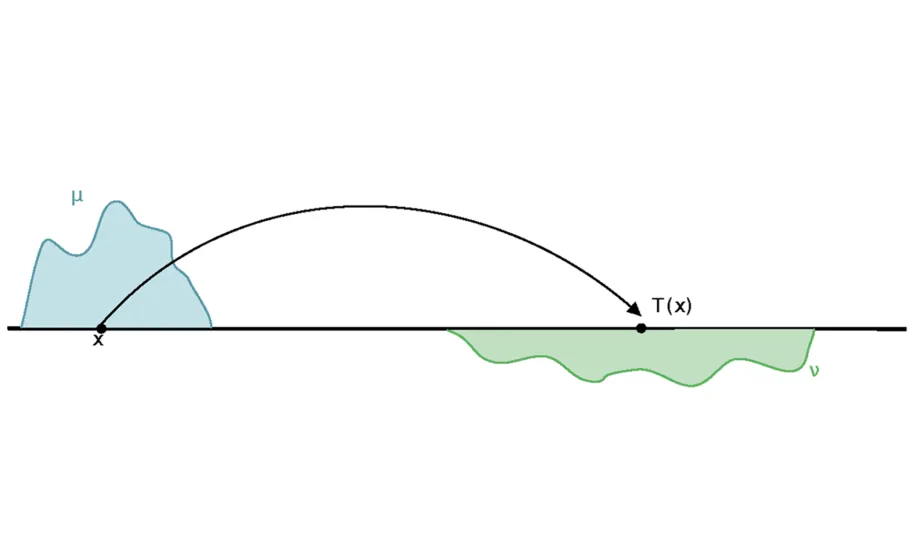
The modern formulation of optimal transport problems is mainly due to the Nobel laureate Leonid Kantorovich [1]. Roughly speaking, they concern the best way to move a given distribution of resources to a prescribed new configuration (Fig. 1). Depending on the meaning assigned to the terms “resource,” “best,” “move,” and “configuration,” one can obtain an amazing variety of different situations: for example optimal allocation of economic resources (the original motivation of Kantorovich’s work that earned him the Nobel Prize), the comparison of probability distributions of random events or statistical data sets, the physical motion of masses or charges, the evolution of particle systems, the modeling of congested crowded motion, the interpolation or generation of images, and so on.
The versatility of the theory [2,3,4] depends on the one hand on its formulation based on general variational principles and on the other on the very powerful combination of measure / probability theory, differential models expressed by partial differential equations, and a geometric perspective. Such a general approach then requires the development of sophisticated numerical methods to be applied to real problems.
The goal of this Focus Group was to bring together the theoretical knowledge of the Fellow and the more application-oriented expertise of the hosts to create a fruitful collaboration while supervising a talented doctoral candidate. This was done along four main directions dealing with optimal transport for unbalanced mass distributions, evolution models for probability measures, new discrete and geometric structures for nonlinear quantum drift diffusion models, and functional analytic and computational tools in probability metric spaces for deep learning.
Figure 1
Unbalanced optimal transport
The classical theory of optimal transport typically concerns moving a given distribution (which mathematically is represented by a finite positive measure) to a target location able to receive precisely the aforementioned quantity of resources (still represented by a positive measure with the same total mass). A very natural and important question is how to describe the same kind of phenomenon in case the problem becomes unbalanced and there may be a gain or a loss of mass during the transport. This is particularly relevant in the case of unnormalized distributions, such as images or more general data. Such a problem has been considered in some specific cases, inspired by a dynamic viewpoint [5,6,7]. We discovered a general approach based on convex relaxation on the metric cone generated by the ambient spaces [8], which is the natural setting for unbalanced optimal transport problems in full generality.
Evolutions of probability measures
Many relevant models for describing the interaction of agents / particles, also in the context of optimization and machine learning, can be represented by the evolution in time of probability measures. A very important class of such evolutions is provided by gradient flows [2], which are driven by suitable functionals and typically converge to their minimum. However, the gradient structure is quite rigid, and even simple perturbations easily destroy such a property. We developed a general notion of evolution that reproduces at the infinite dimensional measure setting some features of more familiar dynamical systems. They are characterized by the notion of measure probability vector fields: Heuristically, each point in the support of a probability measure evolves according to a probability distribution on the space of admissible velocities, whose law is dictated by the nonlocal interaction of the evolving state. This can be thought of as an evolving system in which uncertainty affects both the position and velocity of the particles, depending on some probability distribution. We elaborated on a rather flexible theory that allows for discrete-to-continuous limits and provides a deep connection to the general theory of dissipative evolutions in Hilbert spaces [9,10].
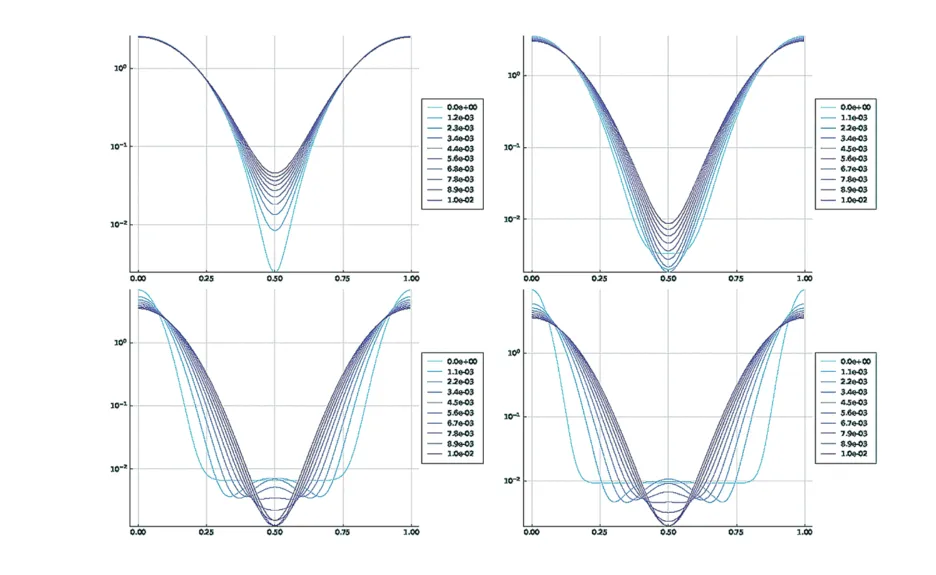
Figure 2
Discrete and geometric structures for nonlinear quantum drift-diffusion models
We addressed the challenging fourth-order Derrida-Lebowitz-Speer-Spohn nonlinear partial differential equation arising in quantum drift-diffusion. Inspired by the geometric and dynamical insights of optimal transport, we introduced [11] a suitable discretization that is able to capture the amazing structures of this remarkable equation, and we also showed a novel gradient flow formulation in terms of a metric that generalizes Martingale transport. The discrete dynamics inherit this gradient flow structure as well as further properties, such as contractivity in the Hellinger distance and monotonicity of several Lyapunov functionals. Using all these features, we are able to perform a precise approximation of the solutions, showing also anti-diffusive behavior and delicate effects when the positive solution approaches 0 at some point (Fig. 2).
Approximation theory, computing, and deep learning on the Wasserstein space
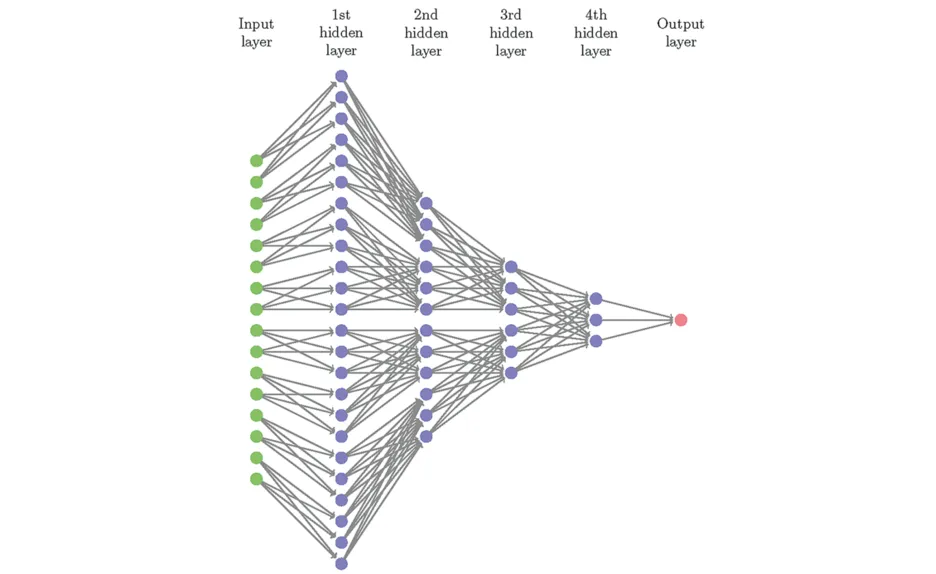
The challenge of approximating functions in infinite-dimensional spaces from finite samples is widely regarded as formidable. We devoted part of our investigation to the problem of the numerical approximation of Sobolev-smooth functions defined on probability spaces. Since measures can be used to represent data in an efficient way and can be used in problems of image comparison or character classification, it is thus relevant to provide a general functional analytic framework.First of all, we studied a notion of Sobolev space on the Wasserstein spaces of probability measures, [12,13] and connected it with the theory of Sobolev spaces in metric measure spaces [14]. We then leveraged the theory of metric Sobolev spaces and combined it with techniques from optimal transport, variational calculus, and large deviation bounds [15]. In our numerical implementation, we used appropriately designed neural networks to serve as basis functions (Fig. 3). This approach allows us to approximate functions that can be rapidly evaluated after training. As a result, our constructive solutions significantly increased the evaluation speed while maintaining the same accuracy, improving state-of-the-art methods by several orders of magnitude.
These themes were at the heart of the workshop Optimal Transport, Mean-Field Models, and Machine Learning (OTMFML), which we organized at the end of the Focus Group activity in collaboration with Martin Burger and Gabriel Peyré. The aim of the workshop was to highlight the interactions between optimal transport, mean-field control, and machine learning, to address the crucial problems of high dimensionality, nonlinearity, and nonconvexity, and to look for best examples and practices of successful use of mathematics to provide guarantees for practicable machine learning.
Figure 3
[1]
Kantorovitch, L. On the translocation of masses. C. R. (Doklady) Acad. Sci. URSS (N.S.) 37, pp. 227–229 (1942).
[2]
Ambrosio, L., Gigli, N. & Savaré, G. Gradient flows in metric spaces and in the space of probability measures. Lectures in Mathematics ETH Zurich (2), pp. x+334. Basel: Birkhäuser Verlag (2008).
[3]
Villani, C. Optimal transport: Old and new. Grundlehren der Mathematischen Wissenschaften (338), pp. xxii+973. Berlin: Springer Verlag (2009).
[4]
Peyré, G. & Cuturi, M. Computational Optimal Transport. Foundations and Trends in Machine Learning 11(5-6), pp. 355–602 (2019).
[5]
Chizat, L., Peyré, G., Schmitzer, B. & Vialard, F.-X. Unbalanced optimal transport: dynamic and Kantorovich formulations. J. Funct. Anal. 274(11), pp. 3090–3123 (2018).
[6]
Kondratyev, S., Monsaingeon, L. & Vorotnikov, D. A new optimal transport distance on the space of finite Radon measures. Adv. Differential Equations 21(11-12), pp. 1117–1164 (2016).
[7]
Liero, M., Mielke, A. & Savaré, G. Optimal entropy-transport problems and a new Hellinger-Kantorovich distance between positive measures. Invent. Math. 211(3), pp. 969–1117 (2018).
[8]
Savaré, G. & Sodini, G.E. (2023).
[9]
Cavagnari, G., Savaré, G. & Sodini, G.E. (2022).
[10]
Cavagnari, G., Savaré, G. & Sodini, G.E. A Lagrangian approach to dissipative evolutions in Wasserstein spaces. arXiv :2305.05211 (2023).
[11]
Matthes, D., Rott, E.-V., Savaré, G. & Schichtling, A. A structure-preserving discretization for the Derrida-Lebowitz-Speer-Spohn equation based on diffusive transport. arXiv:2312.13284 (2023).
[12]
Fornasier, M., Savaré, G. & Sodini, G.E. (2023).
[13]
Sodini, G.E. The general class of Wasserstein Sobolev spaces: density of cylinder functions, reflexivity, uniform convexity and Clarkson’s inequalities. Calculus of Variations and Partial Differential Equations 62, p. 212 (2023).
[14]
Heinonen, J., Koskela, P., Shanmugalingam, N. & Tyson, J.T. Sobolev spaces on metric measure spaces: an appraoch based on upper gradients. New Mathematical Monographs (27), pp. xii+434. Cambridge: Cambridge University Press (2015).
[15]
Fornasier, M., Heid, P. & Sodini, G.E. Approximation Theory, Computing, and Deep Learning on the Wasserstein Space, arXiv:2310.19548 (2023).
Selected publications
- Ambrosio, L., Fornasier, M., Morandotti, M. & Savaré, G. Spatially Inhomogeneous Evolutionary Games. Communications on Pure and Applied Mathematics 74(7), pp. 1353-1402 (2021).
www.doi.org/10.1002/cpa.21995.
- Cavagnari, G., Savaré, G. & Sodini, G.E. Dissipative probability vector fields and generation of evolution semigroups in Wasserstein spaces. Probability Theory and Related Fields (2022).
www.doi.org/10.1007/s00440-022-01148-7.
- Fornasier, M., Savaré, G. & Sodini, G.E. Density of subalgebras of Lipschitz functions in metric Sobolev spaces and applications to Wasserstein Sobolev spaces. Journal of Functional Analysis 285(11), (2023). www.doi.org/10.1016/j.jfa.2023.110153.
- Liero, M., Mielke, A. & Savaré, G. Fine Properties of Geodesics and Geodesic λ-Convexity for the Hellinger-Kantorovich Distance. Arch. Ration. Mech. Anal. 247(6), p. 112 (2023). www.doi.org/10.48550/arXiv.2208.14299.
- Savaré, G. & Sodini, G.E. A relaxation viewpoint to Unbalanced Optimal Transport: duality, optimality and Monge formulation. arXiv:2401.00542 (2023). www.doi.org/10.48550/arXiv.2401.00542.